THE SOLAR SYSTEM - Important definitions to understand Celestial Mechanics and our solar system

HELIOCENTRIC SYSTEM
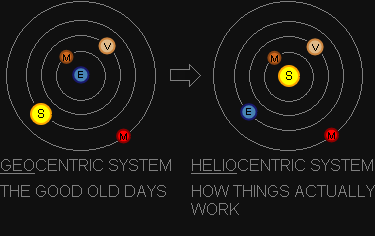Known as a "Sun-centred" model of the solar system with the Earth and the other planets rotating around the sun in circular paths. The word Helio comes from Helios; god of the sun and sunlight [2]. This model was proposed by Nicolaus Copernicus in 1543 [1]. Johannes Kepler was able to mathematically establish by 1627 that the sun-centred model is correct [7]. Until that time the "Earth-centred" model of the solar system was primarily used, where the earth lay "immobile at the center of the rotating universe" [8]. You can see that the simulation has the sun at the center of the solar system, and therefore represents a heliocentric system.
HELIOCENTRIC ECLIPTIC SYSTEM
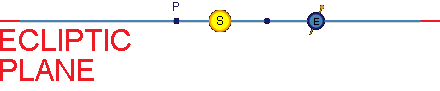A reference system in which the following two conditions apply [10]:
1. The center of the Sun lies at the origin (HELIOCENTRIC)
2. The plane of Earth's orbit defines the reference plane (ECLIPTIC)
The image on the right depicts the "side view" of the solar system using a Heliocentric Ecliptic System. Since the plane of Earth's orbit defines the Ecliptic plane, it lies perfectly "flat".
FIRST POINT OF ARIES
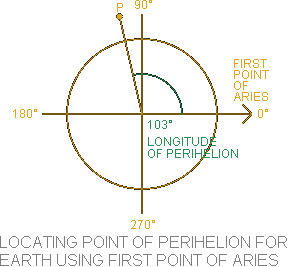Arbitrary fixed direction at a specific moment in time [12] in the reference plane at which the longitude is defined as 0° [11]. For the Heliocentric Ecliptic System this fixed point is defined as the First Point of Aries, and is a vital component for using the orbital elements.
EXAMPLE: From NASA's Planetary Fact Sheet we know that the LONGITUDE OF PERIHELION(ϖ) for Earth was 103° on January 1, 2000 [13]. Using the First Point of Aries as the starting point, we can now determine the position of Earth's perihelion point in its orbit.
The Longitude of Perihelion is measured counter-clockwise from the First Point of Aries [14]. In the illustration on the right, the point of Perihelion for Earth is indicated with the letter "P" at 103°.
THE CELESTIAL SPHERE
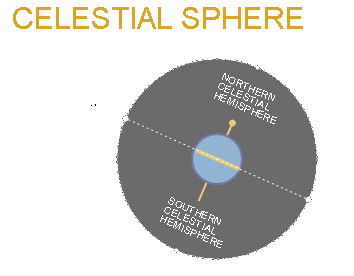On the right you see a graphical representation of the imaginary CELESTIAL SPHERE. It is a sphere that wraps around the Earth and projects the observer's sky on the inside of its dome. The CELESTIAL SPHERE allows observers on Earth to plot positions of objects in the sky (e.g. the sun, stars and planets) using a celestial coordinate system [34].

The Celestial Sphere is split into the Northern and Southern Celestial hemispheres by the Celestial Equator. The Celestial Equator is located at 0° DECLINATION and coincides with the plane of the Earth's equator. This means DECLINATION is analogous to terrestrial latitude [34].

Stars located on the Northeren Celestial hemisphere will have a positive angle of DECLINATION (0° to 90°) and ones with a negative angle will be on the Southern Celestial hemisphere (0° to -90°). No matter where you are on Earth, you can never see more than 180° of sky due to the horizon getting in the way. That also means the only place on Earth where you can see all stars for both Celestial hemispheres, would be if you are on the equator [35].

PATH OF SUN ACROSS SKY
The animation on the right shows the annual path the sun traverses across the sky as seen from Earth for northern hemisphere observers [29].
The animation represents a complete 360° flat projection of the CELESTIAL SPHERE [30] using RIGHT ASCENSION and DECLINATION for its axes.
The apparent "sine wave" that the Sun tracks (shown in yellow) is due to the tilt of the Earth's Axis. This 23.44° tilt is also what causes our seasons, which are depicted using four distinct symbols.

THE ZODIAC
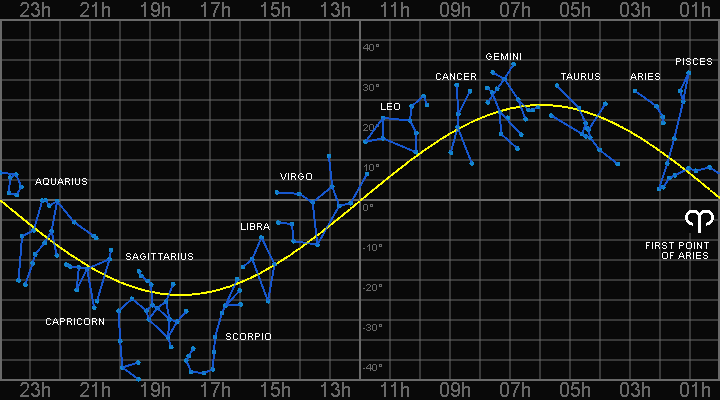The 12 constellations plotted on the Celestial Sphere on the right are known as the Zodiac ("circle of animals"). The sun passes through all 12 during the course of one year. Ancient Astronomers used these constellations to figure out which month of the year it was [31].

Because the sun is so bright, you can't see any other stars during the day. Instead, look to the Eastern sky before sunrise and determine the constellation rising above the horizon. That means the next constellation is where the sun is located [32].

EXAMPLE: If you look East before sunrise on the Northern hemisphere and see the constellation of LEO above the horizon, that means the sun is located in the constellation of VIRGO. This means the date is somewhere between September 16 and October 30 [33].

APPARENT RETROGRADE MOTION
The simulation on the right demostrates the apparent "backwards" motion of the planets in our solar system as seen by observers looking at the night sky.
You would need to take a photo of the planet in question every night over the course of several weeks and then "stack" them on top of each other to see the effect [37].

This apparent retrograde motion of the planets in our solar system is a reflection of the motion of the Earth itself. Retrograde motion can be seen every time one planet "overtakes" the other [36] (see the bottom-right view of the simulation).

EXAMPLE: Mercury overtakes the Earth roughly every 4 months, so you will see 3 "loops" in the simulation over the course of a year. Next to that Venus overtakes the Earth every 20 months and in the case of Mars, the Earth overtakes it every 26 months.
ANOMALY VERSUS LONGITUDE
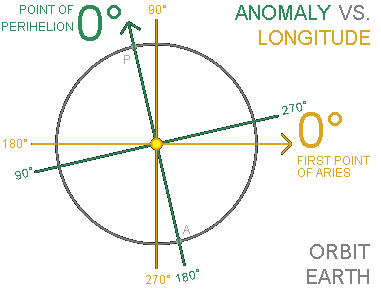When working with orbital elements the terms anomaly and longitude are used a lot.
ANOMALIES are used to describe angles that are important for calculating the position of planets in their orbit around the Sun [26]. Their distinguishing characteristic is that anomalies measure angles since the Point of Perihelion [15]. Therefore 0° represents Perihelion "P" and 180° represents Aphelion "A". In the image on the right the GREEN arrow represents the starting point for measuring anomalies for planet Earth. Examples:
1. MEAN ANOMALY
2. ECCENTRIC ANOMALY
3. TRUE ANOMALY
LONGITUDES are used to describe angles as well and are important in understanding three of the Keplerian elements. Their distinguishing characteristic is that longitudes measure angles since the First Point of Aries [27]. The YELLOW arrow represents the starting point for measuring longitudes. Examples:
1. MEAN LONGITUDE
2. LONGITUDE OF PERIHELION
3. TRUE LONGITUDE

MEAN ANOMALY & TRUE ANOMALY
Mean Anomaly and True Anomaly are terms used to describe planetary positions [16].
The MEAN ANOMALY is the angle measured since the point of perihelion "P" that would have been swept out by the planet if its orbit were perfectly circular (i.e. eccentricity = 0.0) [15]. We call the imaginary planet moving along such an orbit the mean planet [17]. This imaginary planet has a constant velocity and has the same orbital period as the actual planet [16].
The TRUE ANOMALY also measures the angle since the point of perihelion, but represents the actual position of the planet [15]. Of the six orbital elements, only True Anomaly changes continually [18]. The True Anomaly can easily be adjusted to measure the position since First Point of Aries (called the TRUE LONGITUDE).
Before Kepler, orbits were assumed to be circular [19]. Therefore we expected planets to follow the path of the mean planet [20].

TRUE LONGITUDE
True Longitude takes the TRUE ANOMALY of an orbit and adjusts the angle to be measured from First Point of Aries:
TRUE ANOMALY(v) + LONGITUDE OF PERIHELION(ϖ) = TRUE LONGITUDE [21].
EXAMPLE: From JPL's Keplerian Elements we know that the Longitude of Perihelion(ϖ) for Mars was 336.06° on January 1, 2000. This means that the point of Perihelion "P" for Mars is at an angle of 336.06° counter-clockwise from the First Point of Aries (0°).
So if Mars has a TRUE ANOMALY of 23.94° (360° - 336.06°), it will have a TRUE LONGITUDE of 0°.
ORBITAL ELEMENTS
Orbits of the planets in our solar system are described using orbital elements or orbital parameters [22].
They represent the orbit's SIZE, SHAPE, ORIENTATION and POSITION at a given moment in time.
A set of orbital elements therefore represent a snapshot of the planet's orbit around the Sun. Currently January 1, 2000 is the most common "snapshot date" used to represent these orbital elements. This date is also known as the epoch [24]. The traditional or "classical" orbital elements are the six Keplerian elements and are defined HERE.

PERIHELION PRECESSION
When working with the six Orbital Elements, the ones that determine the orbit's SIZE, SHAPE & ORIENTATION slowly change over time due to gravitational forces between the planets. Orbital centennial rates average out the effects of the gravitational forces between planets and represent a linear rate of change from the reference date per century [23].
Find below the rounded orbital centennial rates of the Longitude of Perihelion for the planets in our solar system [28].

MERCURY	VENUS	EARTH	MARS	JUPITER	SATURN	URANUS	NEPTUNE
0.16°	0.06°	0.32°	0.45°	0.18°	0.54°	0.09°	0.01°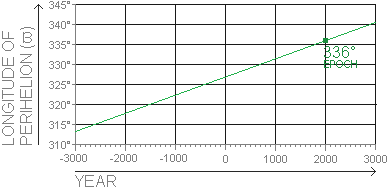

EXAMPLE: From JPL's Keplerian Elements we know that the Longitude of Perihelion (ϖ) for Mars was 336° on January 1, 2000. JPL also gives us the orbital centennial rate of 0.45° per century. This means that the Point of Perihelion will shift by approximately 0.45° per 100 years. This phenomenon is called the Perihelion Precession Rate [25]. The graph plots how the Longitude of Perihelion for Mars shifts over the course of 6000 years.

ASTRONOMICAL NUTATION
A periodic, small, short-term oscillation of the rotational axis of the Earth around its "mean" position. Short-term is defined as ranging from periods less than 10 days, up to 18.6 years [38]. This effect is due to the Earth undergoing torque from external gravitational forces [39]. The majority of these gravitational forces are due to the action of the Moon. Nutation comprises of two components [38]:
1. Nutation in Ecliptic Longitude - Parallel (△ψ)
2. Nutation in Mean Obliquity of the Ecliptic - Perpendicular (△ε)
These two corrections can be applied to the Ecliptic Longitude and Mean Obliquity [40] to find the apparent place of an object in the sky.
PARALLAX

© 2020 NASA

Difference in the apparent position of an object viewed along two different lines of sight. A good example of this is looking at an object in front of you by alternating between closing your left and right eye [41].
Another example is the experiment NASA performed in April 2020 when looking at the closest star system called Alpha Centauri (4.37 light-years). The animation on the right shows one picture of Alpha Centauri taken from Earth and the other taken by the New Horizons space probe at 7 billion kilometers from Earth. These NASA images represent the first Interstellar Parallax Experiment [45].
(LUNAR) GEOCENTRIC PARALLAX ANGLE
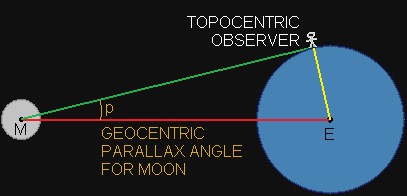The angular difference in the apparent direction or position of a celestial body as observed from the center of the earth (geocentric) and from a point on the surface of the earth (topocentric) [38].
The Moon has a relatively large parallax compared to other celestial bodies, due to its close proximity to Earth and can exceed 1° [42]. The maximum geocentric parallax angle is observed when the celestial body is located at the observer's horizon (0°) [43]. This maximum value is called horizontal parallax, which represents the maximum possible shift [44].
ELLIPSE
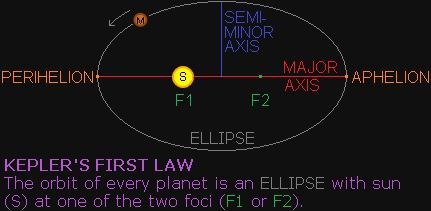All planets in our solar system follow elliptical orbits around the sun [3]. An ellipse is basically a circle that has been "squashed" to look like an oval. It's eccentricity determines how squashed it is. If the eccentricity = 0, then it is a perfect circle. If the eccentricity = 1, then it has been flattened to a line [6]. Earth for example has an eccentricity of 0.0167; almost a perfect circular orbit. Mercury has an orbit which is much more eccentric at 0.2056 [4]. The eccentricity of the orbit influences the orbital speed of a planet. An ellipse has two "foci" [5]. The sun lies at one of the foci. The point in its orbit closest to the sun is called "perihelion". The point in its orbit furthest away from the sun is called "aphelion".
PERIHELION
Nearest point of a body's orbit around the sun. Indicated in the simulation with the letter "P". This is the point at which the planet has the highest velocity. Conservation of Angular Momentum by Isaac Newton tells us that as the distance between the planet and the sun decreases, the velocity must increase proportionally [9].
For Mercury this highest velocity is 58.98km/s [4]. In the simulation you can clearly see the planet speed up and slow down as it orbits the sun.
APHELION
Farthest point of a body's orbit around the sun. Indicated in the simulation as a grey point in its orbit (exactly 180° from the point of perihelion). This is the point at which the planet has the lowest velocity. For Mercury this is 38.86km/s [4]. So that means the velocity difference between perihelion and aphelion for Mercury is 20.12km/s, which translates to roughly 70,000km/h difference.
FOCI
Every ellipse has two foci (plural of focus). The foci lie on the major axis, equally spaced from the center of the ellipse. A circle has both foci at the center. For planets within our solar system, the sun lies in one of its foci [6].
MAJOR AXIS
The major axis of an ellipse is either the horizontal or vertical line that runs along its longest diameter from perihelion to aphelion. It also runs through the center and both foci [6].
SEMI-MINOR AXIS
The semi-minor axis is a line that runs at a 90° angle of the major axis from the center of the ellipse to either end (shortest radius) [5].

REFERENCES
[1] What Is The Difference Between the Geocentric and Heliocentric Models of the Solar System, Howell, E. (2015)
[2] Helios (Helius, Sol, Sun), Šimon, B. (no date)
[3] Why do planets have elliptical orbits, Slater, S. (2016)
[4] Planetary Fact Sheet, NASA (2016)
[5] Foci (focus points) of an ellipse, Math Open Reference (2011)
[6] Introductory Astronomy: Ellipses, Worthey, G. (2001)
[7] The Fall of the Geocentric Theory, and the Rise of Heliocentrism, Harrison, T. (no date) BROKEN LINK
[8] Ptolemaic Astronomy in the Middle Ages, Mahoney, M.S. (no date)
[9] Gravity and Orbits, Thompson, T. (2014)
[10] Space Navigation Handbook, NAVPERS (1961)
[11] First Point in Aries, Weisstein, E.W. (1996-2007) BROKEN LINK
[12] First Point of Aries, Academic Kids (no date)
[13] Earth Fact Sheet, NASA (2016)
[14] Orbital Mechanics, Braeunig, R.A. (1997)
[15] Orbit Anomalies, Earl, M.A. (2010)
[16] Solving Kepler's Equation of Elliptical Motion, Giesen, J. (2016)
[17] Solving Kepler’s Equation and Calculating the Positions of the Planets, Colarusso, D. (2004)
[18] True Anomaly, Sellers, J. J. (no date) BROKEN LINK
[19] The Copernican Model: A Sun-Centered Solar System, Blackman, E.G. (no date)
[20] Orbits in 2D, Kirkman, T. (no date)
[21] True Longitude, Weisstein, E.W. (1996-2007) BROKEN LINK
[22] DEFINITION OF ORBITAL PARAMETERS, Polytechnic University of Catalonia (no date)
[23] Computing planet positions using mean orbital elements, Schmitt, S.R. (2005)
[24] Keplerian Elements in Detail, AMSAT (2004, 2016)
[25] Perihelion precession rate, Fitzpatrick, F. (2016)
[26] Astronomical Dictionary, Strous, L. (2017)
[27] Eclipse, Nave, R. (no date)
[28] Perihelion Precession of the Planets, Fitzpatrick, F. (2011)
[29] The Ecliptic: the Sun's Annual Path on the Celestial Sphere, Durham University (no date)
[30] The Ecliptic – A Trace of the Sun’s Path across the Celestial Sphere, Jim Johnson (2015)
[31] The Dendera Zodiac, Ancient Origins (2017)
[32] The Path of the Sun, the Ecliptic, NASA (2014)
[33] The Real Constellations of the Zodiac, Dr. Lee T. Shapiro (1977)
[34] The Celestial Sphere, The Center for Planetary Science (no date)
[35] Introduction to Astronomy, Bishop University (2001)
[36] Astronomy Picture of the Day, NASA (2001)
[37] Astronomy Picture of the Day, NASA (2003)
[38] Astronomical Algorithms, Meeus, J. (1999)
[39] SSD Glossary: Nutation, NASA (1992)
[40] Practical Astronomy With Your Calculator, Duffett-Smith, P. (1988)
[41] Lunar Parallax: Estimating the Moon's Distance, Wright, E. (no date)
[42] American Practical Navigator, Bowditch, N (1966)
[43] Encyclopædia Britannica, Encyclopædia Britannica, Inc. (2020)
[44] Notes on the Calculation of Geocentric Parallax, Beyond the Horizon (no date)
[45] NASA’s New Horizons Conducts the First Interstellar Parallax Experiment, NASA (2020)