During his lifetime, Johannes Kepler defined three laws that correctly describe the motion of the planets orbiting the sun [1]. The first two laws of planetary motion were published in 1609 based on observations of the planet Mars. The third law was published ten years later in 1619. Kepler died in 1630 at the age of 58, after a string of forced relocations due to his religious beliefs [5].
The laws explained on this page have been used to create the JS Simulation of the Solar System on this website.

I. LAW OF ORBITS

ORBIT SIZE & ORBIT SHAPE

ORBIT ORIENTATION (3 ELEMENTS)

• III. INCLINATION
  The angle at which the ORBITAL PLANE of a planet is tilted relative to the plane of reference (or fundamental plane). A plane is a flat 2D surface that extends into infinity. In our solar system, the plane of reference is called the ECLIPTIC PLANE [8]. The ecliptic plane is defined by the apparent path the sun takes through the sky during the course of a year as seen from Earth [15]. This implies that Earth has a 0.0° INCLINATION. Earth's EQUATORIAL PLANE has a 23.4° degree angle with the ecliptic. In the illustration it can be seen that Mars has a 1.85° INCLINATION. Therefore the orbital plane of Mars is very close to that of Earth. As a matter of fact all planets in our solar systems have closely related orbital planes, making the solar system relatively "flat" [9]. This is because all planets were formed out of a disk of dust surrounding the sun that was all in one plane [10].
  NOTE: It is important not to confuse the axial tilt of the planets in our solar system with the orbital inclination. The axial tilt of Mars is 25.19° but it's inclination to the plane of reference is only 1.85°.
• IV. LONGITUDE OF THE ASCENDING NODE
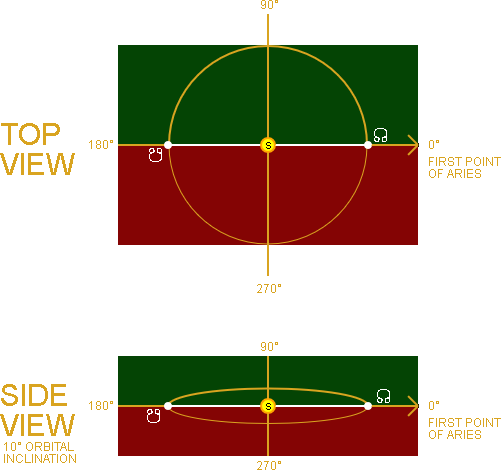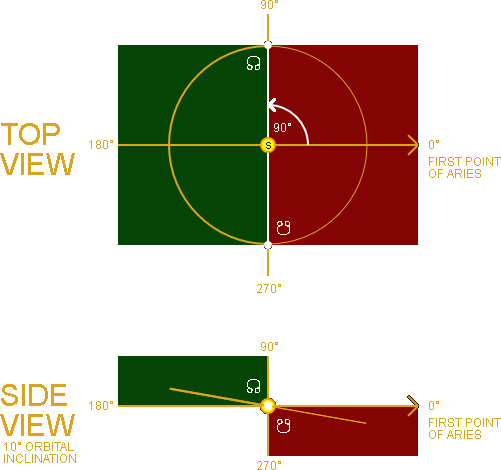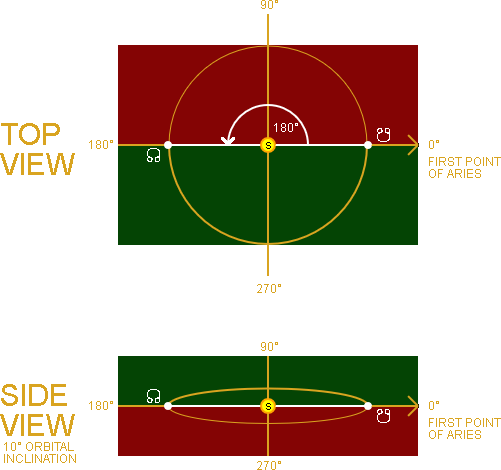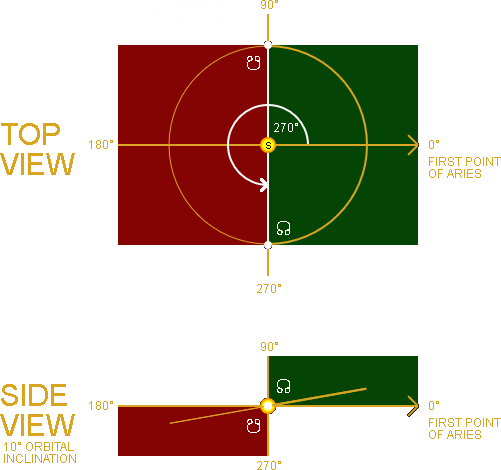  The second orbital element that "fixes" the orbital plane in space is the Longitude of the Ascending Node [17]. This is the point in its orbit, measured counter-clockwise from the First Point of Aries, where the orbital plane crosses the ecliptic plane going "upward" [12].
  
  In the animation on the right you can see what the Longitude of the Ascending Node (Ω) looks like at 0°, 90°, 180° and 270°.
  In this example the imaginary planet's orbital plane has an inclination of 10° with the ecliptic. Half the orbit is above the ecliptic (GREEN) and the other half is below the ecliptic (RED).
  
  The WHITE line connecting the two nodes is called the line of nodes. This is the intersection between the orbital plane and the ecliptic plane. This intersection with the ecliptic can best be seen in the side view at 90° and 270°.

V. LONGITUDE OF PERIHELION
The last element that specifies the orientation of the orbit is the Longitude of Perihelion (ϖ). This element represents the angular rotation of the elliptical orbit [6] around the sun to the Point of Perihelion (i.e. point of closest approach to sun) [18]. The First Point of Aries is the origin of longitude (0°) and the angle is measured counter-clockwise [19].
The example on the right shows how the Point of Perihelion is rotated around the Sun by adjusting the angle.
EXAMPLE: Jupiter has its Point of Perihelion at 14.8° and Mars at 336° [19].
Your browser does not support HTML5 Canvas. Please update your browser.

ORBIT POSITION

• VI. MEAN LONGITUDE
  Finally, the Mean Longitude is the angle of the planet in its orbit, starting from the First Point of Aries and measured counter-clockwise. This Mean Longitude will only be correct if the orbit is perfectly circular. Since we know by now that the planets in our Solar System are NOT circular but elliptical, this angle cannot be used to accurately position the planets.
  
  Instead, using the Mean Longitude as our starting point, we can convert it to the "true" angle using a three-step process [21]:
  1. Adjust MEAN LONGITUDE to represent MEAN ANOMALY
  2. Calculate ECCENTRIC ANOMALY from MEAN ANOMALY using iterative procedure
  3. Convert ECCENTRIC ANOMALY to TRUE ANOMALY
  
  The True Anomaly is the actual angular measure of the planet in its orbit, starting from the Point of Perihelion. This angle is also measured counter-clockwise between 0° and 360°. The Point of Aphelion therefore represents a value of 180° as it lies on the opposite side of orbit. This "true" angle is the angle used in the simulation.

Now that we have briefly discussed all SIX orbital elements, we can take the next step and see what they actually look like for the planets in our Solar System.

The table below lists a snapshot of these elements taken on January 1st, 2000 for the planet Mars. As mentioned, the first five elements barely change over time, that is why we called them elements. Subtle changes to the first five elements are caused by gravitational forces between the planets [21]. Only the Mean Longitude changes rapidly as Mars orbits the Sun: 191.4° per year to be exact. This makes sense as its orbital period is 1.87 years.

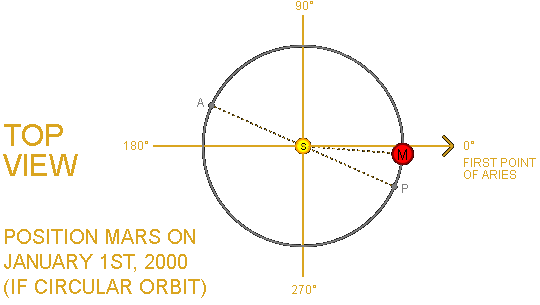
EXAMPLE: So what can we easily derive from the data in this table? Let's focus on the last two orbital elements.
Imagine a top-down view of the Solar System (just like the simulation) and follow these steps using pen and paper:

1. Start by drawing the Sun at the center and the orbit of Mars around it.
2. Now set the First Point of Aries due East by drawing a horizontal arrow through the Sun: this is our longitude of origin (0°).
3. By looking at the LONGITUDE OF PERIHELION (ϖ0), we know that its Point of Perihelion lies 336.06° counter-clockwise from the longitude of origin. Mark this point within its orbit and indicate with the letter "P".
4. Next mark the Point of Aphelion with the letter "A" located 180° from perihelion.
5. Finally draw the location of the planet Mars itself for January 1st, 2000 using the MEAN LONGITUDE (L0). Mars was located at 355.45° counter-clockwise from First Point of Aries at that time. So Mars just recently passed its Point of Perihelion and has almost completed a full orbit.
   NOTE: For simplicity we assume that the orbit of Mars is circular; so we can use the Mean Longitude directly.

II. LAW OF AREAS

III. LAW OF PERIODS