THE SOLAR SYSTEM - Important definitions to understand our solar system

HELIOCENTRIC SYSTEM
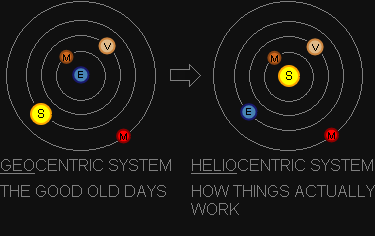Known as a "Sun-centred" model of the solar system with the Earth and the other planets rotating around the sun in circular paths. The word Helio comes from Helios; god of the sun and sunlight [2]. This model was proposed by Nicolaus Copernicus in 1543 [1]. Johannes Kepler was able to mathematically establish by 1627 that the sun-centred model is correct [7]. Until that time the "Earth-centred" model of the solar system was primarily used, where the earth lay "immobile at the center of the rotating universe" [8]. You can see that the simulation has the sun at the center of the solar system, and therefore represents a heliocentric system.
HELIOCENTRIC ECLIPTIC SYSTEM
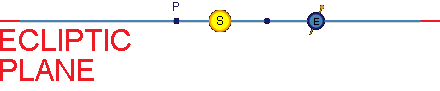A reference system in which the following two conditions apply [10]:
1. The center of the Sun lies at the origin (HELIOCENTRIC)
2. The plane of Earth's orbit defines the reference plane (ECLIPTIC)
The image on the right depicts the "side view" of the solar system using a Heliocentric Ecliptic System. Since the plane of Earth's orbit defines the Ecliptic plane, it lies perfectly "flat".
FIRST POINT OF ARIES
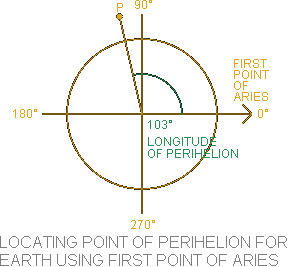Arbitrary fixed direction at a specific moment in time [12] in the reference plane at which the longitude is defined as 0° [11]. For the Heliocentric Ecliptic System this fixed point is defined as the First Point of Aries, and is a vital component for using the orbital elements.
EXAMPLE: From NASA's Planetary Fact Sheet we know that the LONGITUDE OF PERIHELION(ϖ) for Earth was 103° on January 1, 2000 [13]. Using the First Point of Aries as the starting point, we can now determine the position of Earth's perihelion point in its orbit.
The Longitude of Perihelion is measured counter-clockwise from the First Point of Aries [14]. In the illustration on the right, the point of Perihelion for Earth is indicated with the letter "P" at 103°.
ANOMALY VERSUS LONGITUDE
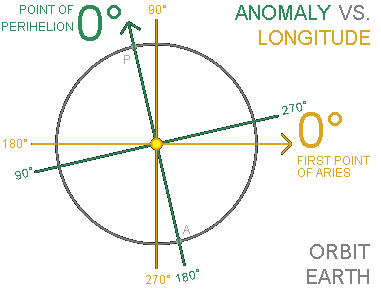When working with orbital elements the terms anomaly and longitude are used a lot.
ANOMALIES are used to describe angles that are important for calculating the position of planets in their orbit around the Sun [26]. Their distinguishing characteristic is that anomalies measure angles since the Point of Perihelion [15]. Therefore 0° represents Perihelion "P" and 180° represents Aphelion "A". In the image on the right the GREEN arrow represents the starting point for measuring anomalies for planet Earth. Examples:
1. MEAN ANOMALY
2. ECCENTRIC ANOMALY
3. TRUE ANOMALY
LONGITUDES are used to describe angles as well and are important in understanding three of the Keplerian elements. Their distinguishing characteristic is that longitudes measure angles since the First Point of Aries [27]. The YELLOW arrow represents the starting point for measuring longitudes. Examples:
1. MEAN LONGITUDE
2. LONGITUDE OF PERIHELION
3. TRUE LONGITUDE

MEAN ANOMALY & TRUE ANOMALY
Mean Anomaly and True Anomaly are terms used to describe planetary positions [16].
The MEAN ANOMALY is the angle measured since the point of perihelion "P" that would have been swept out by the planet if its orbit were perfectly circular (i.e. eccentricity = 0.0) [15]. We call the imaginary planet moving along such an orbit the mean planet [17]. This imaginary planet has a constant velocity and has the same orbital period as the actual planet [16].
The TRUE ANOMALY also measures the angle since the point of perihelion, but represents the actual position of the planet [15]. Of the six orbital elements, only True Anomaly changes continually [18]. The True Anomaly can easily be adjusted to measure the position since First Point of Aries (called the TRUE LONGITUDE).
Before Kepler, orbits were assumed to be circular [19]. Therefore we expected planets to follow the path of the mean planet [20].

TRUE LONGITUDE
True Longitude takes the TRUE ANOMALY of an orbit and adjusts the angle to be measured from First Point of Aries:
TRUE ANOMALY(v) + LONGITUDE OF PERIHELION(ϖ) = TRUE LONGITUDE [21].
EXAMPLE: From JPL's Keplerian Elements we know that the Longitude of Perihelion(ϖ) for Mars was 336.06° on January 1, 2000. This means that the point of Perihelion "P" for Mars is at an angle of 336.06° counter-clockwise from the First Point of Aries (0°).
So if Mars has a TRUE ANOMALY of 23.94° (360° - 336.06°), it will have a TRUE LONGITUDE of 0°.
ORBITAL ELEMENTS
Orbits of the planets in our solar system are described using orbital elements or orbital parameters [22].
They represent the orbit's SIZE, SHAPE, ORIENTATION and POSITION at a given moment in time.
A set of orbital elements therefore represent a snapshot of the planet's orbit around the Sun. Currently January 1, 2000 is the most common "snapshot date" used to represent these orbital elements. This date is also known as the epoch [24]. The traditional or "classical" orbital elements are the six Keplerian elements and are defined HERE.

PERIHELION PRECESSION
When working with the six Orbital Elements, the ones that determine the orbit's SIZE, SHAPE & ORIENTATION slowly change over time due to gravitational forces between the planets. Orbital centennial rates average out the effects of the gravitational forces between planets and represent a linear rate of change from the reference date per century [23].
Find below the rounded orbital centennial rates of the Longitude of Perihelion for the planets in our solar system [28].

MERCURY	VENUS	EARTH	MARS	JUPITER	SATURN	URANUS	NEPTUNE
0.16°	0.06°	0.32°	0.45°	0.18°	0.54°	0.09°	0.01°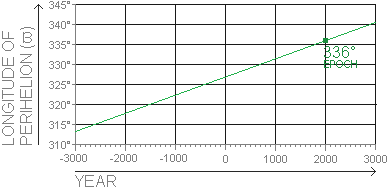

EXAMPLE: From JPL's Keplerian Elements we know that the Longitude of Perihelion (ϖ) for Mars was 336° on January 1, 2000. JPL also gives us the orbital centennial rate of 0.45° per century. This means that the Point of Perihelion will shift by approximately 0.45° per 100 years. This phenomenon is called the Perihelion Precession Rate [25]. The graph plots how the Longitude of Perihelion for Mars shifts over the course of 6000 years.

ELLIPSE
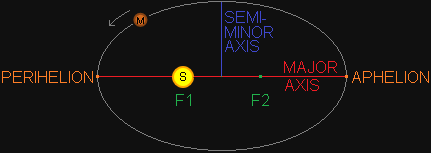All planets in our solar system follow elliptical orbits around the sun [3]. An ellipse is basically a circle that has been "squashed" to look like an oval. It's eccentricity determines how squashed it is. If the eccentricity = 0, then it is a perfect circle. If the eccentricity = 1, then it has been flattened to a line [6]. Earth for example has an eccentricity of 0.0167; almost a perfect circular orbit. Mercury has an orbit which is much more eccentric at 0.2056 [4]. The eccentricity of the orbit influences the orbital speed of a planet. An ellipse has two "foci" [5]. The sun lies at one of the foci. The point in its orbit closest to the sun is called "perihelion". The point in its orbit furthest away from the sun is called "aphelion".
PERIHELION
Nearest point of a body's orbit around the sun. Indicated in the simulation with the letter "P". This is the point at which the planet has the highest velocity. Conservation of Angular Momentum by Isaac Newton tells us that as the distance between the planet and the sun decreases, the velocity must increase proportionally [9].
For Mercury this highest velocity is 58.98km/s [4]. In the simulation you can clearly see the planet speed up and slow down as it orbits the sun.
APHELION
Farthest point of a body's orbit around the sun. Indicated in the simulation as a grey point in its orbit (exactly 180° from the point of perihelion). This is the point at which the planet has the lowest velocity. For Mercury this is 38.86km/s [4]. So that means the velocity difference between perihelion and aphelion for Mercury is 20.12km/s, which translates to roughly 70,000km/h difference.
FOCI
Every ellipse has two foci (plural of focus). The foci lie on the major axis, equally spaced from the center of the ellipse. A circle has both foci at the center. For planets within our solar system, the sun lies in one of its foci [6].
MAJOR AXIS
The major axis of an ellipse is either the horizontal or vertical line that runs along its longest diameter from perihelion to aphelion. It also runs through the center and both foci [6].
SEMI-MINOR AXIS
The semi-minor axis is a line that runs at a 90° angle of the major axis from the center of the ellipse to either end (shortest radius) [5].

REFERENCES
[1] What Is The Difference Between the Geocentric and Heliocentric Models of the Solar System, Howell, E. (2015)
[2] Helios (Helius, Sol, Sun), Šimon, B. (no date)
[3] Why do planets have elliptical orbits, Slater, S. (2016)
[4] Planetary Fact Sheet, NASA (2016)
[5] Foci (focus points) of an ellipse, Math Open Reference (2011)
[6] Introductory Astronomy: Ellipses, Worthey, G. (2001)
[7] The Fall of the Geocentric Theory, and the Rise of Heliocentrism, Harrison, T. (no date)
[8] Ptolemaic Astronomy in the Middle Ages, Mahoney, M.S. (no date)
[9] Gravity and Orbits, Thompson, T. (2014)
[10] Space Navigation Handbook, NAVPERS (1961)
[11] First Point in Aries, Weisstein, E.W. (1996-2007)
[12] First Point of Aries, Academic Kids (no date)
[13] Earth Fact Sheet, NASA (2016)
[14] Orbital Mechanics, Braeunig, R.A. (1997)
[15] Orbit Anomalies, Earl, M.A. (2010)
[16] Solving Kepler's Equation of Elliptical Motion, Giesen, J. (2016)
[17] Solving Kepler’s Equation and Calculating the Positions of the Planets, Colarusso, D. (2004)
[18] True Anomaly, Sellers, J. J. (no date)
[19] The Copernican Model: A Sun-Centered Solar System, Blackman, E.G. (no date)
[20] Orbits in 2D, Kirkman, T. (no date)
[21] True Longitude, Weisstein, E.W. (1996-2007)
[22] DEFINITION OF ORBITAL PARAMETERS, Polytechnic University of Catalonia (no date)
[23] Computing planet positions using mean orbital elements, Schmitt, S.R. (2005)
[24] Keplerian Elements in Detail, AMSAT (2004, 2016)
[25] Perihelion precession rate, Fitzpatrick, F. (2016)
[26] Astronomical Dictionary, Strous, L. (2017)
[27] Eclipse, Nave, R. (no date)
[28] Perihelion Precession of the Planets, Fitzpatrick, F. (2011)